 |
Google OR-Tools v9.15
a fast and portable software suite for combinatorial optimization
|
 |
Google OR-Tools v9.15
a fast and portable software suite for combinatorial optimization
|
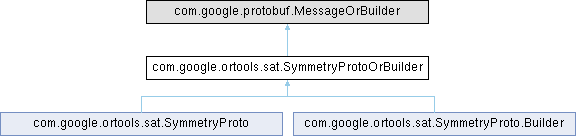
Definition at line 9 of file SymmetryProtoOrBuilder.java.
Public Member Functions | |
| java.util.List< com.google.ortools.sat.SparsePermutationProto > | getPermutationsList () |
| com.google.ortools.sat.SparsePermutationProto | getPermutations (int index) |
| int | getPermutationsCount () |
| java.util.List<? extends com.google.ortools.sat.SparsePermutationProtoOrBuilder > | getPermutationsOrBuilderList () |
| com.google.ortools.sat.SparsePermutationProtoOrBuilder | getPermutationsOrBuilder (int index) |
| java.util.List< com.google.ortools.sat.DenseMatrixProto > | getOrbitopesList () |
| com.google.ortools.sat.DenseMatrixProto | getOrbitopes (int index) |
| int | getOrbitopesCount () |
| java.util.List<? extends com.google.ortools.sat.DenseMatrixProtoOrBuilder > | getOrbitopesOrBuilderList () |
| com.google.ortools.sat.DenseMatrixProtoOrBuilder | getOrbitopesOrBuilder (int index) |
| com.google.ortools.sat.DenseMatrixProto com.google.ortools.sat.SymmetryProtoOrBuilder.getOrbitopes | ( | int | index | ) |
An orbitope is a special symmetry structure of the solution space. If the variable indices are arranged in a matrix (with no duplicates), then any permutation of the columns will be a valid permutation of the feasible space. This arise quite often. The typical example is a graph coloring problem where for each node i, you have j booleans to indicate its color. If the variables color_of_i_is_j are arranged in a matrix[i][j], then any columns permutations leave the problem invariant.
repeated .operations_research.sat.DenseMatrixProto orbitopes = 2;
Implemented in com.google.ortools.sat.SymmetryProto.Builder, and com.google.ortools.sat.SymmetryProto.
| int com.google.ortools.sat.SymmetryProtoOrBuilder.getOrbitopesCount | ( | ) |
An orbitope is a special symmetry structure of the solution space. If the variable indices are arranged in a matrix (with no duplicates), then any permutation of the columns will be a valid permutation of the feasible space. This arise quite often. The typical example is a graph coloring problem where for each node i, you have j booleans to indicate its color. If the variables color_of_i_is_j are arranged in a matrix[i][j], then any columns permutations leave the problem invariant.
repeated .operations_research.sat.DenseMatrixProto orbitopes = 2;
Implemented in com.google.ortools.sat.SymmetryProto.Builder, and com.google.ortools.sat.SymmetryProto.
| java.util.List< com.google.ortools.sat.DenseMatrixProto > com.google.ortools.sat.SymmetryProtoOrBuilder.getOrbitopesList | ( | ) |
An orbitope is a special symmetry structure of the solution space. If the variable indices are arranged in a matrix (with no duplicates), then any permutation of the columns will be a valid permutation of the feasible space. This arise quite often. The typical example is a graph coloring problem where for each node i, you have j booleans to indicate its color. If the variables color_of_i_is_j are arranged in a matrix[i][j], then any columns permutations leave the problem invariant.
repeated .operations_research.sat.DenseMatrixProto orbitopes = 2;
Implemented in com.google.ortools.sat.SymmetryProto.Builder, and com.google.ortools.sat.SymmetryProto.
| com.google.ortools.sat.DenseMatrixProtoOrBuilder com.google.ortools.sat.SymmetryProtoOrBuilder.getOrbitopesOrBuilder | ( | int | index | ) |
An orbitope is a special symmetry structure of the solution space. If the variable indices are arranged in a matrix (with no duplicates), then any permutation of the columns will be a valid permutation of the feasible space. This arise quite often. The typical example is a graph coloring problem where for each node i, you have j booleans to indicate its color. If the variables color_of_i_is_j are arranged in a matrix[i][j], then any columns permutations leave the problem invariant.
repeated .operations_research.sat.DenseMatrixProto orbitopes = 2;
Implemented in com.google.ortools.sat.SymmetryProto.Builder, and com.google.ortools.sat.SymmetryProto.
| java.util.List<? extends com.google.ortools.sat.DenseMatrixProtoOrBuilder > com.google.ortools.sat.SymmetryProtoOrBuilder.getOrbitopesOrBuilderList | ( | ) |
An orbitope is a special symmetry structure of the solution space. If the variable indices are arranged in a matrix (with no duplicates), then any permutation of the columns will be a valid permutation of the feasible space. This arise quite often. The typical example is a graph coloring problem where for each node i, you have j booleans to indicate its color. If the variables color_of_i_is_j are arranged in a matrix[i][j], then any columns permutations leave the problem invariant.
repeated .operations_research.sat.DenseMatrixProto orbitopes = 2;
Implemented in com.google.ortools.sat.SymmetryProto.Builder, and com.google.ortools.sat.SymmetryProto.
| com.google.ortools.sat.SparsePermutationProto com.google.ortools.sat.SymmetryProtoOrBuilder.getPermutations | ( | int | index | ) |
A list of variable indices permutations that leave the feasible space of solution invariant. Usually, we only encode a set of generators of the group.
repeated .operations_research.sat.SparsePermutationProto permutations = 1;
Implemented in com.google.ortools.sat.SymmetryProto.Builder, and com.google.ortools.sat.SymmetryProto.
| int com.google.ortools.sat.SymmetryProtoOrBuilder.getPermutationsCount | ( | ) |
A list of variable indices permutations that leave the feasible space of solution invariant. Usually, we only encode a set of generators of the group.
repeated .operations_research.sat.SparsePermutationProto permutations = 1;
Implemented in com.google.ortools.sat.SymmetryProto.Builder, and com.google.ortools.sat.SymmetryProto.
| java.util.List< com.google.ortools.sat.SparsePermutationProto > com.google.ortools.sat.SymmetryProtoOrBuilder.getPermutationsList | ( | ) |
A list of variable indices permutations that leave the feasible space of solution invariant. Usually, we only encode a set of generators of the group.
repeated .operations_research.sat.SparsePermutationProto permutations = 1;
Implemented in com.google.ortools.sat.SymmetryProto.Builder, and com.google.ortools.sat.SymmetryProto.
| com.google.ortools.sat.SparsePermutationProtoOrBuilder com.google.ortools.sat.SymmetryProtoOrBuilder.getPermutationsOrBuilder | ( | int | index | ) |
A list of variable indices permutations that leave the feasible space of solution invariant. Usually, we only encode a set of generators of the group.
repeated .operations_research.sat.SparsePermutationProto permutations = 1;
Implemented in com.google.ortools.sat.SymmetryProto.Builder, and com.google.ortools.sat.SymmetryProto.
| java.util.List<? extends com.google.ortools.sat.SparsePermutationProtoOrBuilder > com.google.ortools.sat.SymmetryProtoOrBuilder.getPermutationsOrBuilderList | ( | ) |
A list of variable indices permutations that leave the feasible space of solution invariant. Usually, we only encode a set of generators of the group.
repeated .operations_research.sat.SparsePermutationProto permutations = 1;
Implemented in com.google.ortools.sat.SymmetryProto.Builder, and com.google.ortools.sat.SymmetryProto.